The simplest and the most well-defined contact mechanics problem is the contact between a ball (radius R) and a flat surface. For this problem two limiting cases can be solved exactly, namely the case of an elastically soft contact with large radius R, where the Johnson–Kendall–Roberts (JKR) [K. L. Johnson, K. Kendall and A. D. Roberts, Surface Energy and the Contact of Elastic Solids, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313] theory is valid, and that of an elastically hard contact with small radius R, where the Derjaguin–Muller–Toporov (DMT) [B. V. Derjaguin, V. M. Muller and Y. P. Toporov, Effect of Contact Deformations on the Adhesion of Particles, J. Colloid Interface Sci., 1975, 53, 314–326] theory is valid.
The contact region between a spherical probe (radius R) and a flat rubber surface is circular with a radius r. The interaction between the solids is described by the work of adhesion w, which is the energy per unit surface area necessary to separate two flat surfaces from their equilibrium contact position to infinite separation. According to the JKR theory the relation between the force F and the radius r on the stable branch of the interaction curve is

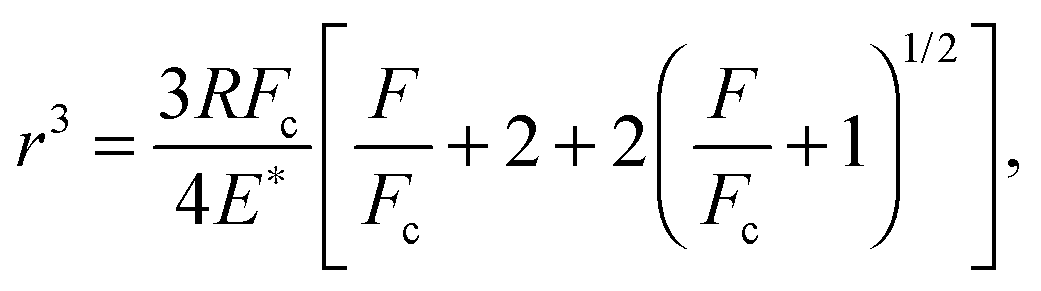
where E^* = E/(1 − ν²), and E and ν are the rubber's Young's modulus and Poisson's ratio, respectively, and

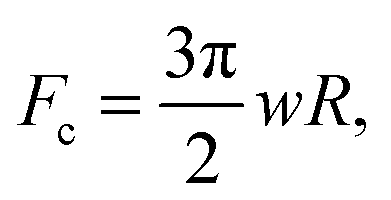
is the maximum pull-off force.
Thus for an elastic solid, if the ball is pulled by a soft spring (and neglecting inertia effects), at F=−F_c the pull-off force abruptly drops to zero.
It is well known that the separation line r = r(t) can be considered as a crack tip. The work of adhesion w in general depends on the velocity v_r = ṙ of the opening (during pull-off) or closing (during contact formation) crack. At finite crack velocity, for an opening crack w can be strongly enhanced, and for a closing crack it is strongly reduced, compared to the adiabatic (infinitely low crack tip velocity) value w₀. One contribution to the work of adhesion is derived from the viscoelastic energy dissipation in the vicinity of the crack tip (see the figure below). For an opening crack this will enhance w with a factor 1 + f(v_r,T), which depends on the crack tip velocity v_r and the temperature T. For a closing crack the corresponding reduction factor is approximately ≈1/(1 + f(v_r,T)) as described in [E. Barthel and C. Frétigny, Adhesive Contact of Elastomers: Effective Adhesion Energy and Creep Function, J. Phys. D: Appl. Phys., 2009, 42, 195302].
The figure below shows a rigid ball pulled away from a viscoelastic solid. A part of the energy needed to remove the ball is derived from viscoelastic energy dissipation inside the rubber close to the opening crack tip (red dashed region).

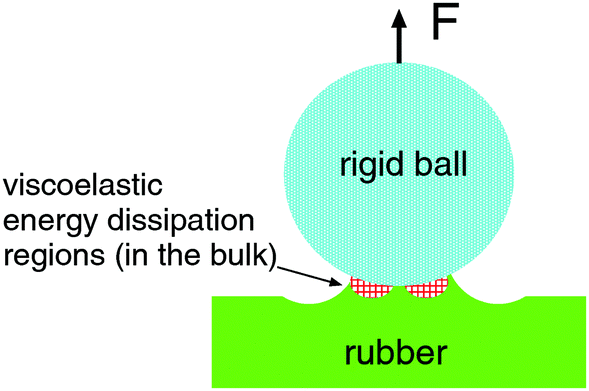
The JKR theory assumes elastic solids, and it is not clear a priori if it can be applied to viscoelastic solids like rubber. However, if the elastic deformation field far away from the crack can be treated as elastic, and if the pull-off velocity is not too high, one expects the JKR theory to hold also for viscoelastic solids.
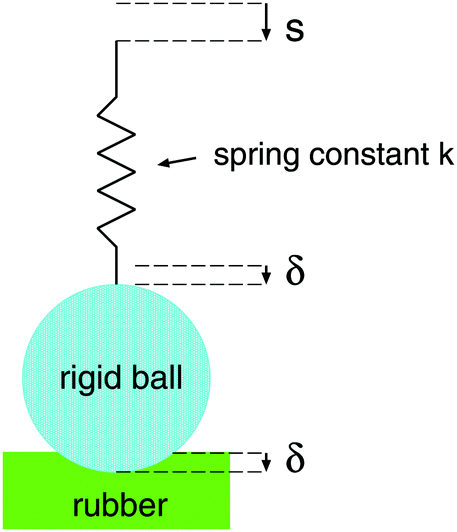
In the present set-up the probe ball can be, e.g. a soda-lime silica glass ball with diameter 4 cm or 2.5 cm. In this case the drive can be represented by a relatively soft spring, and the contact region is not observed directly but only the time dependency of the interaction force F(t) and the displacement s(t) of the upper part of the driving spring are measured, see the figure below:

Since the work of adhesion depends on the crack tip velocity v_r=dr(t)/dt we need to determine this quantity. We can calculate v_r from the time dependency of F(t) assuming that the JKR theory is valid. We can obtain r(t) from the measured F(t). During pull-off the velocity v_r varies with time, but what is most important is the velocity at the point when the pull-off force is maximal; this is the crack velocity quoted below.
There is a second way one can derive the velocity v_r, namely from the time dependency of the vertical displacement of the drive. Thus using the JKR relation between the penetration δ and the radius r of the contact region,

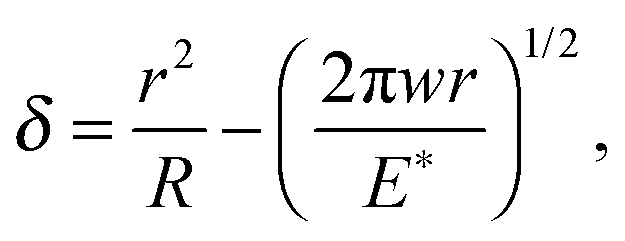
one can show that at pull-off (F=−F_c) [B. Lorenz, B. Krick, N. Mulakaluri, M. Smolyakova, S. Dieluweit, W. Sawyer and B. Persson, Adhesion: Role of Bulk Viscoelasticity and Surface Roughness, J. Phys.: Condens. Matter, 2013, 25, 225004]

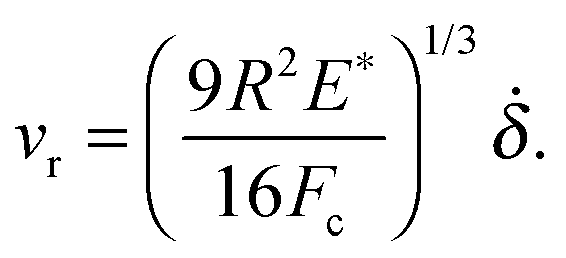
However, this equation can be used only if the penetration δ(t) is known. If the drive is rigid (or stiff enough) δ(t) is equal (or near equal) to the drive displacement s(t). In the present set-up where an effective spring separates the drive from the glass ball (see the figure above). If the spring constant is denoted by k, then k(s−δ)=F.
In the present set-up one can bring, e.g. a glass ball (with diameter 2R≈4 cm) into contact with a soft substrate as shown in the figure below. It is positioned on a very accurate analytical balance which has a reproducibility up to 0.1 mg, which means ≈1 μN (customizable). After zeroing the scale of the instrument we can measure the force on the substrate as a function of time which is directly transferred to a computer at a rate up to 10 data points per second (customizable, depends on the balance option).

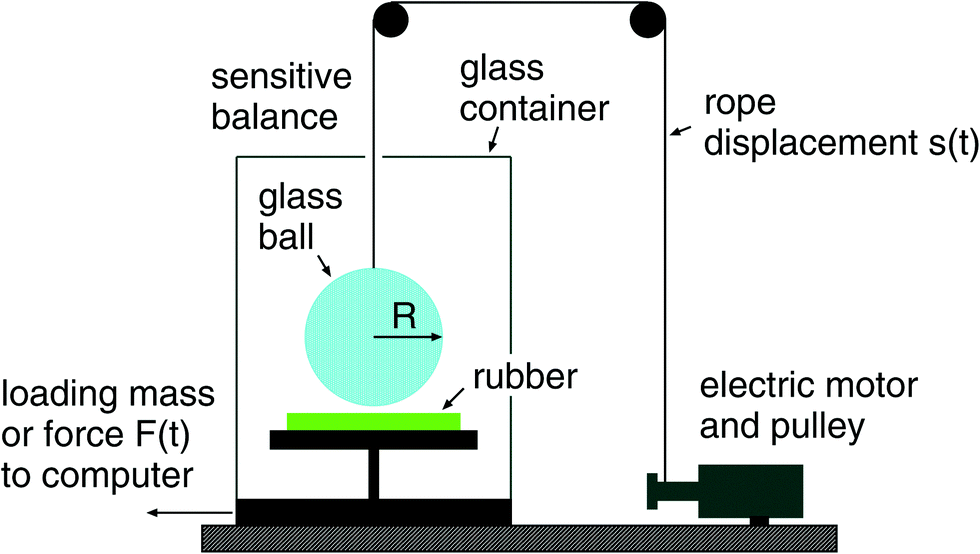
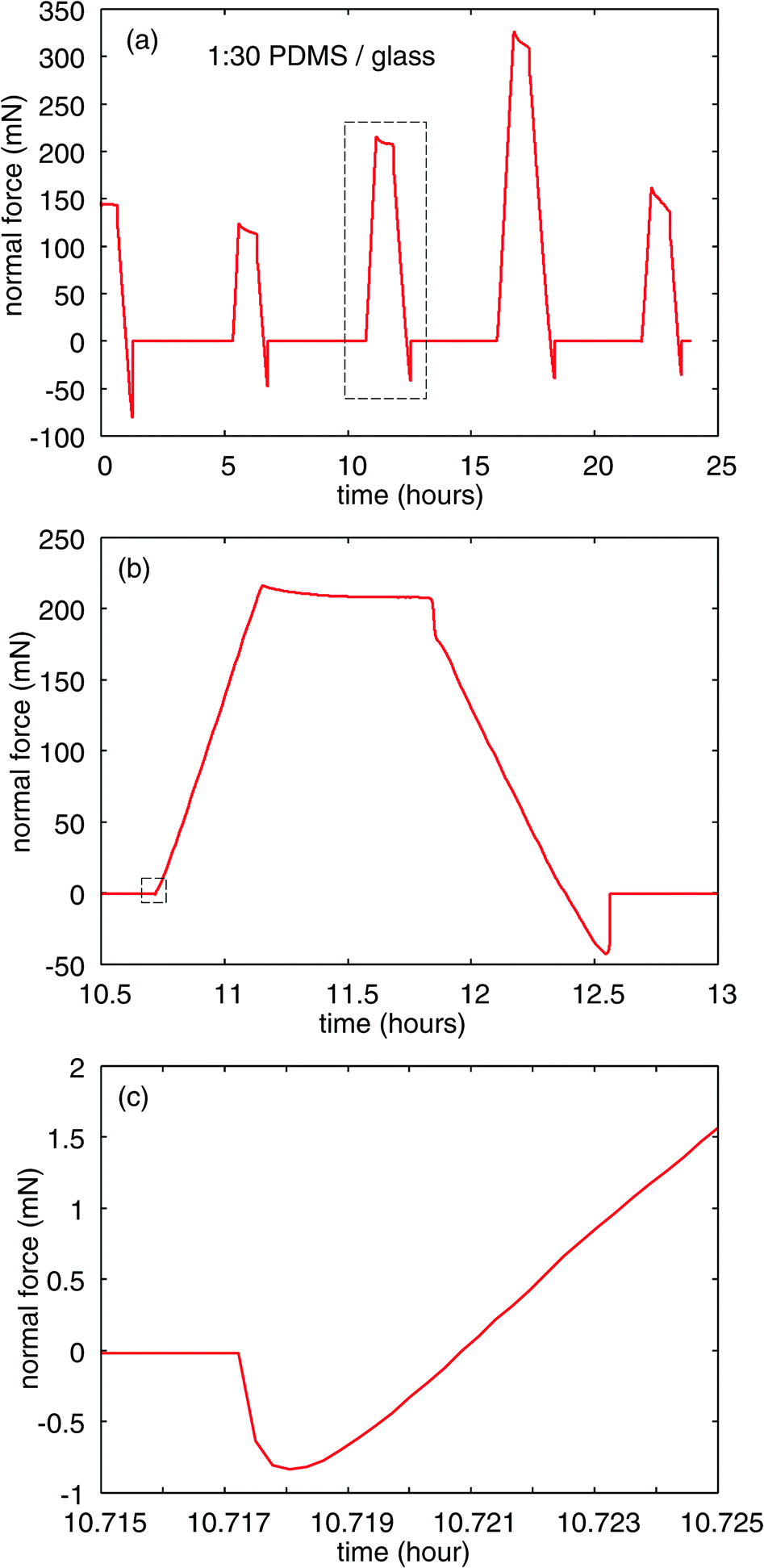
To move the glass ball up and down there is an electric motor coiling up a nylon cord, which is attached to the ball. The rigid ball is repeatedly moved up and down with specified speed. The figure below shows a typical force–time curve during one contact cycle.

It is important that the instrument can operate by automatically repeated cycles with the following set of parameter that defines each cycle:

• driving speed ds(t)/dt;
• driving range ;
• contact hold time T₁;
• delay time in the summit T₂.

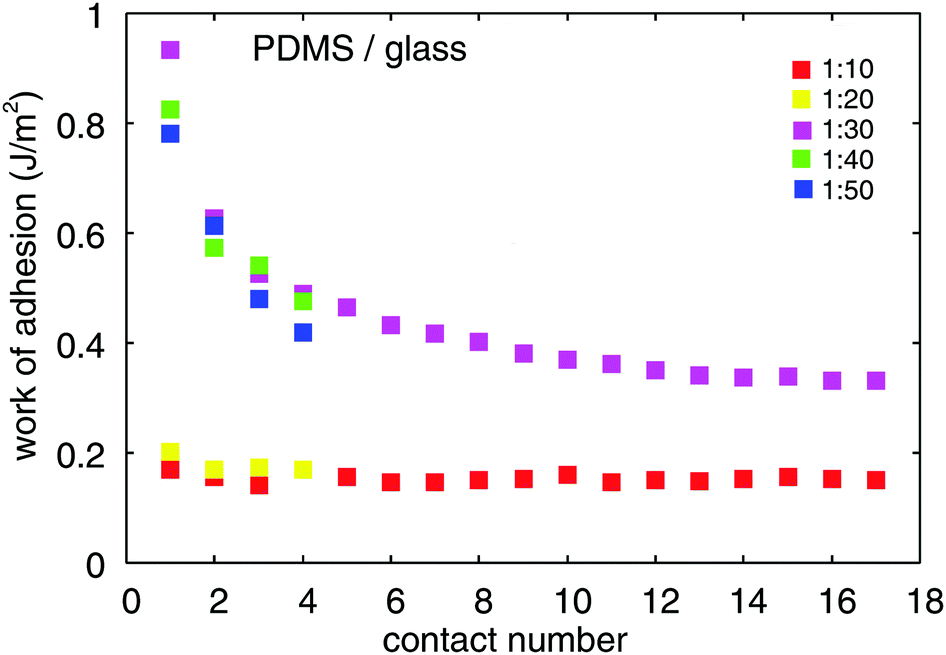
These repeated contacts happening in the same contact spot can evidence the contamination of contact surfaces and adhesion wear, as illustrated in the figure below for PDMS substration versus glass:

The adhesion tester based on Mettler Toledo MS104TS/00 analytical balance:

The present instrument had been successfully applied for various types of elastomers, as described in the following academic papers.

We can produce an adhesion tester by order, or carry out service measurements of adhesion for your materials. For details, please contact us.

1. A. Tiwari, L. Dorogin, A.I. Bennett, K.D. Schulze, W.G. Sawyer, M. Tahir, G. Heinrich, and B.N.J. Persson, "The effect of surface roughness and viscoelasticity on rubber adhesion"; Soft Matter 13 (2017) 3602-3621, DOI: 10.1039/C7SM00177K
2. L. Dorogin, A. Tiwari, C. Rotella, P. Mangiagalli, and B.N.J. Persson, "Role of preload in adhesion of rough surfaces"; Phys. Rev. Lett. 118, 238001 (2017).
3. A. Tiwari, L. Dorogin, M. Tahir, K. W. Stöckelhuber, G. Heinrich, N. Espallargas and B. N. J. Persson, "Rubber contact mechanics: adhesion, friction and leakage of seals"; Soft Matter (2017), DOI: 10.1039/C7SM02038D
4. L. Dorogin and B. N. J. Persson, "Contact mechanics for polydimethylsiloxane: from liquid to solid", Soft Matter, 2018,14, 1142-1148, DOI:10.1039/C7SM02216F