Contact mechanics and friction are both topics of huge importance with many applications in Nature and technology. They are closely interconnected, so that understanding friction requires a deep insight into the contact formation between two solids. Rubber friction is of practical importance, e.g., for tire applications, syringes, and wiper blades. However, it is also a topic of great complexity. Until recently there did not exist a physical model describing the energy dissipation mechanisms when a rubber block slides on a hard rough substrate. We at Multiscale Consulting use the Persson contact mechanics approach to understand rubber friction in more detail. Here we have developed a model which is used today to calculate friction in the context of tires and other applications.

Understanding rubber friction is of crucial importance especially in the context of tires.

Earlier studies of rubber friction on rough surfaces have indicated that there are several contributions to rubber friction. We believe that only from a detailed experimental study of several different systems (different types of rubber and substrate surfaces) under different sliding conditions (velocity and temperature) will it be possible to gain quantitative insight into the relative importance of the various contributions to rubber friction. We believe that there are several different origins for rubber friction which can become important depending on the system under investigation and the prevailing conditions. The figure below illustrates our current understanding of rubber friction.

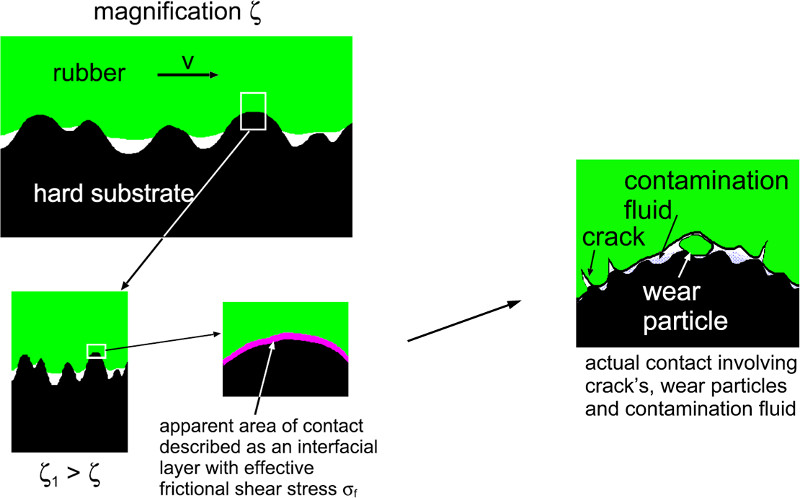
Consider a rubber block in relative motion with a hard, randomly rough substrate. The road asperities will induce pulsating deformations of the rubber, resulting in viscoelastic energy dissipation in the bulk of the rubber which gives an important contribution to the friction. We refer to this dissipation mechanism as viscoelastic friction or hysteretic (bulk) contribution. Note that because of the nature of surface roughness to occur over different length scales the rubber gets deformed on different length scales. Increasing the magnification we find smaller and smaller roughness components resulting in higher frequencies. At a particular magnification this effect brakes down due to high temperatures and stresses prevailing in the contacting regions. Here the rubber molecule network brakes so that it cannot contribute to the viscoelastic mechanism any more. The second mechanism we have identified is the shearing of the apparent area of contact at that particular magnification. Here we will refer to as shearing of the contact area or adhesive (surface) contribution. Below we will now discuss these two effects in more detail.

When a rubber block is sliding on a hard rough substrate the surface asperities of the substrate will exert fluctuating forces on the rubber surface which, because of the internal friction of the rubber, will result in energy transfer from the translational motion of the block into the irregular thermal motion (see FIGURE below). This will result in a contribution to the friction force acting on the rubber block. The energy dissipation will result in local heating of the rubber. Since the viscoelastic properties of rubber-like materials are extremely strongly temperature dependent, it is necessary to include the local temperature increase when calculating the friction force. Recently Persson has developed a theory which accurately describes this energy dissipation process, and which predicts the velocity dependence (and, in a more general case, the time history dependence) of the rubber friction coefficient. The results depend only on the (complex) viscoelastic modulus E(omega) of the rubber, and on the substrate surface roughness power spectra C(q).
Here we also take into account the flash temperature effect, a very localized increase in temperature in a finite rubber volume due to energy dissipation. The flash temperature happens also only on small time scales, however they will via diffusion of temperature into the rubber bulk also heat up the background temperature of the rubber. As the rubber properties, and hence also the frictional properties, are strongly temperature sensitive this effect should not be neglected. We have developed a theory which can take into account both of these two effects on rubber friction.

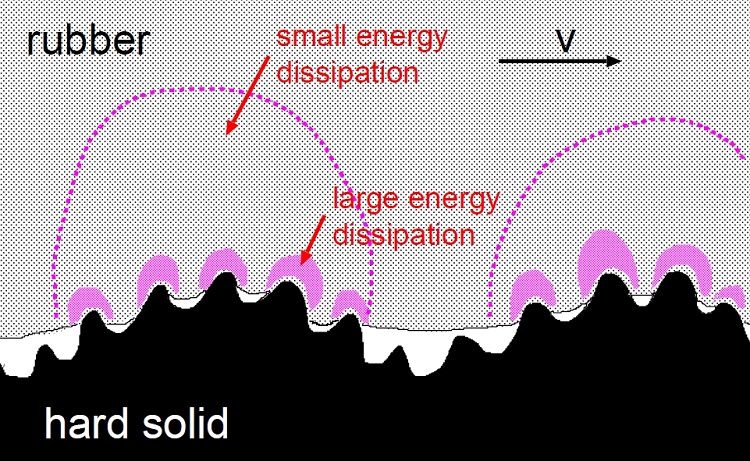Viscoelastic deformation of the rubber due to surface roughness asperities of the substrate on two different length scales. The dissipated energy per unit volume is largest in the small asperity contact regions.

The adhesive contribution results from the attractive binding forces between the rubber surface and the substrate. Surface forces are often dominated by weak attractive van der Waals interactions. When the applied squeezing force on two very smooth substrates is very gentle, this weak attraction may result in a nearly complete contact at the interface, leading to the large sliding friction force usually observed. This happens because of the low elastic modulus of rubber-like materials allowing large areas of contact. For rough surfaces the adhesive contribution to rubber friction will be much smaller because of the small contact area. The actual contact area between a tire and the road surface, for example, is typically only ≈1% of the nominal footprint contact area. Under these conditions the bulk (hysteretic) friction mechanism is believed to prevail. For example, the exquisite sensitivity of tyre–road friction to temperature reflects the strong temperature dependence of the viscoelastic bulk properties of rubber.

However we found that there is a contribution from the surfaces interacting with each other in our experimental studies. The frictional shear stress acting in the area of contact is therefore an effective shear stress associated with the contact between a rather ill-defined rubber layer and the road surface. It is clear that only a combined experimental–theory approach can determine the nature of the frictional shear stress acting in the area of contact.

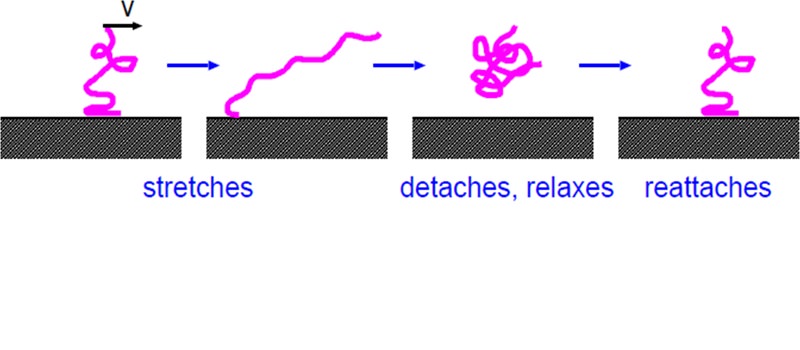
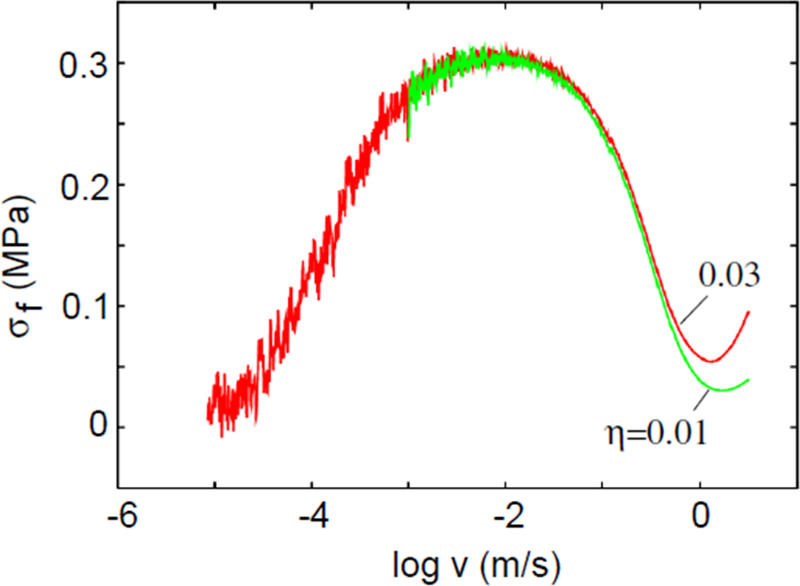
Supposed dissipation mechanism when shearing the contact area. Rubber molecules bind to the substrate, get stretched until the bond breaks. The elastic energy used for stretching the bond is dissipated when the molecules return to their lowest energy state where they are relaxed and more compact again. Then the molecule tries to bind to the substrate again and the cycle is repeated.	The shear stress acting in the contact regions as a function of velocity (with log10 as basis). Note the Gaussian behaviour of the shear stress with a maximum at of order centimetre per second and a broad function over 4 decades in velocity at half maximum. Also typical is the decrease in shear stress at higher and lower velocities which has to do with associated the bond braking process.

When we did this study mentioned above, we identified the following dissipation mechanism. Suppose a rubber block is sliding on a substrate, the rubber molecules in the contact region will try to find a good binding spot on the substrate as this might be energetically favourable. However the rubber bulk will continue to move relative to the substrate so that the rubber molecule gets stretched or elongated as illustrated in the figure above, left side. At some time the elastic energy which gets stored up in the rubber molecule while elongating is so strong as to brake the bond between the molecule and the substrate. When this happens, the molecule will return back to its energetically more favourable situation and curl up to a more compact state. The elastic energy which gets released during this process gets dissipated. After detaching and relaxing, the molecule will try to reattach to the substrate by finding a good binding region again. This closes the binding-stretching-detaching-relaxing-reattaching cycle again and the whole process repeats itself. The shear stress acting in the contact regions associated with this process is shown in the upper figure on the right side.

A broad Gaussian-like curve can be observed with a maximum typically at velocities of order centimetre per second. The width of this curve at half maximum is of order 4 decades in velocity while the shear stress decreases for higher and also lower velocities. This can be explained with the following arguments. At higher velocities, the rubber slides over the substrate quicker which makes it less likely for the molecule to find a good binding position resulting in less molecules bound to the substrate and hence a decrease in the effective shear stress. This happens because the rubber molecule needs some time in order to move around until it finds a good binding position. The higher the velocity the less molecules binding with the substrate. At high enough velocity this contribution to the total friction coefficient might be completely removed as eventually no molecules are bound anymore.

For lower velocities a decrease in the shear stress is also expected as seen in the figure above, right side. The reason for this is the following. The bond between the rubber molecule and the substrate can either be broken because of elastic energy accumulating in the molecule or due to thermal excitations giving a kick to the molecule which is large enough to help braking the bond. The lower the velocity of the rubber, the higher the probability for a thermal excited bond braking becomes and hence the shear stress decreases with decreasing velocity.

We at Multiscale Consulting have found this process in the contact regions to be of importance for rubber friction at lower velocities and have included this effect in our theories. Depending on the system under investigation, there might also be other mechanisms which contribute to the friction. We refer you to our publications to learn more about this.

The total rubber friction is the sum of the hysteretic, or viscoelastic, contribution and the contact area contribution as follows:

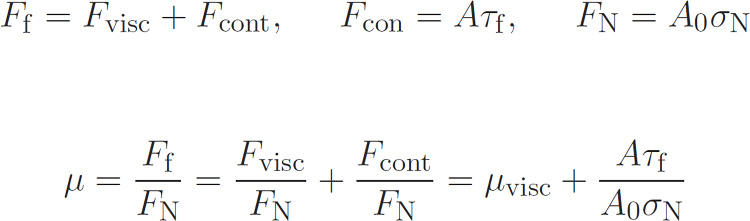
The contact area contribution is written as contact area times a frictional shear force. The normal force is the nominal contact area times the normal stress. Thus the friction coefficient is the viscoelastic friction coefficient plus the true contact times the frictional shear stress divided by the nominal contact times the normal stress. Our theory approach calculates the viscoelastic contribution when the power spectrum and the material properties are known. Note that in this approach are no fitting or open parameters which could be used to manipulate the result. The nominal contact area is known as well as the normal stress. The contact area at the particular magnification where shearing the interface becomes important is calculated by the Persson contact mechanics theory and the shear stress acting is assumed based on earlier experimental studies of this quantity.

We have tested this approach on rubber friction using the Persson theories both numerically and experimentally. Up to know we have observed good agreement with the theory predictions and the calculated or measured results. To illustrate this we show in the figure below the measured friction coefficient of a tread rubber block sliding on a road surface at low sliding velocities and at 15°C temperature. The experiment was first performed on dry surfaces resulting in the red points. As the surface roughness power spectrum as well as the complex viscoelastic modulus were both known, it was possible to estimate the friction coefficient for this system. The lower green curves are the viscoelastic contribution to the friction with and without flash temperature effect (dotted and solid line). The upper green curves are the total friction coefficient as explained above. Here the two contributions from the viscoelastic deformations of the rubber and the shearing of the wear layer are both added together.

We see that the predictions for the friction are in very good agreement with the experimental results. To further test the effect of the shearing of the contact water has been added to remove surface interactions. This resulted in the blue crosses. It seems as if the water does not get completely squeezed-out from the contact but partly separates the rubber-road interface with a thin water layer hence removing any surface interactions. However the water could not remove this effect completely which is referred to the fact that water partly stays in the contact. In another experiment soap was added to the water which helps forming a thin layer in the contact which separates the two surfaces from each other. Note that the separating layer is also thin enough to not influence the viscoelastic energy dissipation in the rubber.

Adding soap to the water it was possible to fully remove any surface interactions. The measured friction coefficient (blue boxes) agree nicely with the theory predictions for the viscoelastic contribution alone.

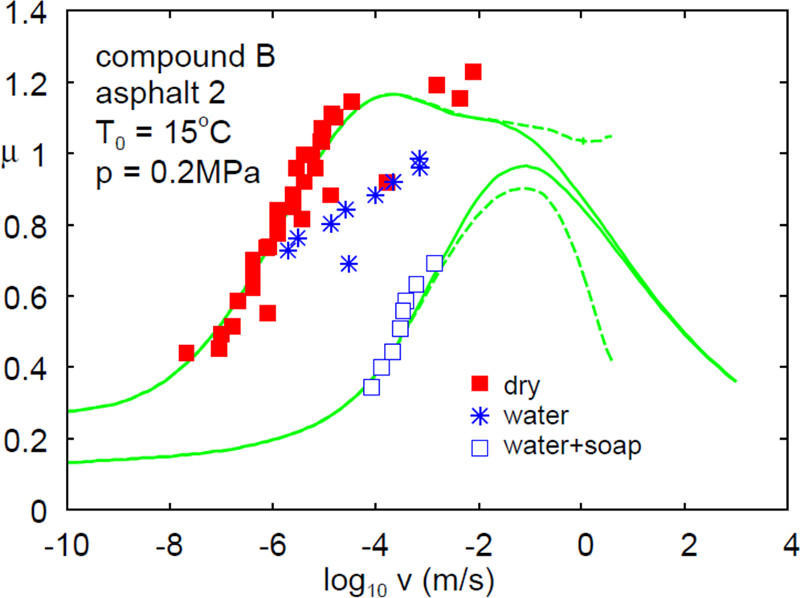Measured (dots) and calculated (lines) friction coefficient for rubber sliding on a road surface. The lower green curves are the viscoelastic contribution to the friction while the upper green curves are the total friction coefficient including the shearing of the contact. Note the good agreement between experiment and theory for dry surfaces. Adding a water-soap mixture reduced the measured friction by completely removing any surface interactions (adhesive friction). Only the viscoelastic contribution is left which agrees also very well with the predicted results from the theory.

In case you want to learn more about the validation of the theory please visit our validation section. The codes which have been written during the development of the approach is also available as software.

If you are interested in using the contact mechanics program or you have further questions concerning the theory please feel free to contact us.